In mathematics, a hypergeometric series is a power series in which the ratios of successive coefficients k is a rational function of k. The series, if convergent, will define a hypergeometric function which may then be defined over a wider domain of the argument by analytic continuation. Hypergeometric functions generalize many special functions, including the Bessel functions, the incomplete Gamma function, the error function, the elliptic integrals and the orthogonal polynomials. This is in part because the hypergeometric functions are solutions to the hypergeometric differential equation, which is a fairly general second-order ordinary differential equation.
The ordinary hypergeometric series should not be confused with the basic hypergeometric series, which, despite its name, is a rather more complicated and less frequently studied series. The basic series is the q-analog of the ordinary hypergeometric series. There are several generalizations of the ordinary hypergeometric series, including a generalization to Riemann symmetric spaces.

The series 2F1
Several of the familiar elementary functions can be expressed in terms of the hypergeometric function ₂F₁. These include

Elementary functions
The classic orthogonal polynomials can all be expressed as special cases of with one or both a and b being (negative) integers. Many other special cases are listed in the Category:Special hypergeometric functions.
The function ₂F₁ has several integral representations, including the Euler hypergeometric integral.
Applications of hypergeometric series include the inversion of elliptic integrals; these are constructed by taking the ratio of the two linearly independent solutions of the hypergeometric differential equation to form Schwarz-Christoffel maps of the fundamental domain to the complex projective line or Riemann sphere.
A wide range of integrals of simple functions can be expressed using the hypergeometric function, e.g.:

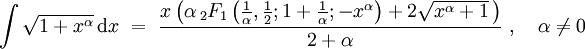
A limiting case of ₂F₁ is the Kummer function ₁F₁(a,b;z), known as the confluent hypergeometric function.

Special cases and applications
In the general case, the hypergeometric series is written as:

where α₀ = 1 and

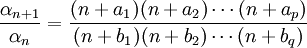
The series may also be written:

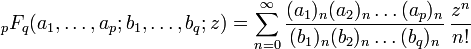
where (a)_n = a(a + 1)(a + 2)...(a + n − 1) is the rising factorial or Pochhammer symbol.

The series pFq
A number of hypergeometric function identities were discovered in the nineteenth and twentieth centuries; one classical list of such identities is Bailey's list.
It is currently understood that there is a very large number of such identities, and several algorithms are now known to generate and prove these identities. Some mathematicians research the various patterns that emerge from these algorithms.

Formal definition
The standard notation for the general hypergeometric series is

Here, the integers m and p refer to the degree of the polynomials P and Q, respectively, referring to the ratio

If m>p+1, the radius of convergence is zero and so there is no analytic function. The series naturally terminates in case P(n) is ever 0 for n a natural number. If Q(n) were ever zero, the coefficients would be undefined.
The full notation for F assumes that P and Q are monic and factorised, so that the notation for F includes an m-tuple that is the list of the negatives of the zeroes of P and a p-tuple of the negatives of the zeroes of Q. This is not much of a restriction: the fundamental theorem of algebra applies, and we can also absorb a leading coefficient of P or Q by redefining z. As a result of the factorisation, a general term in the series then takes the form of a ratio of products of Pochhammer symbols. Since Pochhammer notation for rising factorials is traditional it is neater to write F with the negatives of the zeros. Thus, to complete the notational example, one has

where (a)_n = a(a + 1)(a + 2)...(a + n − 1) is the rising factorial or Pochhammer symbol. Here, the zeros of P were −a and −b, while the zero of Q was −c.

History and generalizations